20220106-朱刘算法

发表于 更新于 阅读次数： 本文字数： 1.1k 阅读时长 ≈ 1 分钟

朱刘算法

0. 背景

  • 无向图：最小生成树；
  • 有向图：最小树形图；

  • 联系：如果把一个树形图的有向边替换成无向边，它会变成一棵生成树。但不同于生成树，树形图中会确定一个根，它必须满足根能够到达每个结点。最小树形图是所有树形图中边权和最小的一个。

    首先我们知道 【树】的根节点没有入边 出边可以无限多，而其他节点出边也可以无限多 但入边只有一条。

    既然要所有点都在树内 我们就贪心地选取所有入点u的边中权值最小的。

    如果此时能形成一棵树 那无疑就是最优解,可以直接直觉认为 当前选的n-1条边中没有边成环就能形成树.

    如果有环我们就进行缩点 【把在同一个环内的点看成一个点 同时更新指向环中任意一点的边权】

    qaq

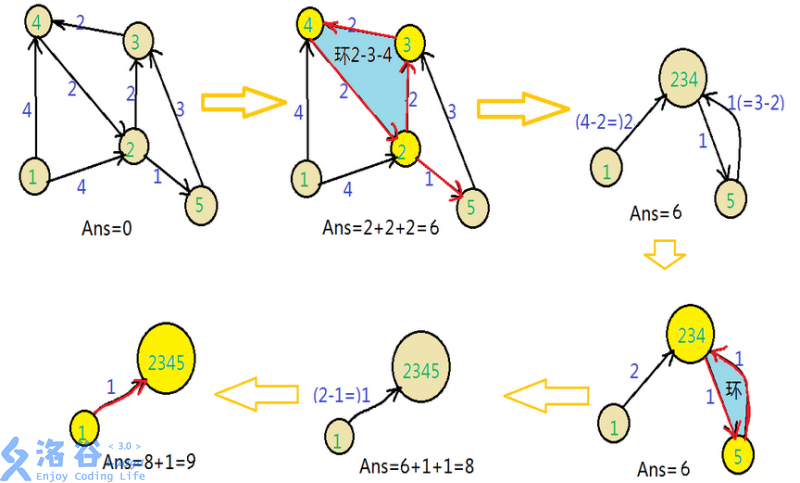
1. 算法

  • 基本思想：每次贪心地选出每个点最小的父亲，得出的图如果不是树形图，那么将选出的环进行缩点，对边权进行修改，然后迭代这个过程，直到图变为最小树形图为止。

  • Tarjan优化（懒惰删除法🐕）：

    • 朱刘相当于最小生成树中B字开头的算法,而现在介绍的优化，其实相当于prim。
    • 枚举每个原图中的节点x，然后不停地把边(pre[x],x)加入最小树形图，答案累加in[x]，在某一时刻发现出现了环，删除该环内部所有边，然后暴力把每个指向该环的边(u,v)，令边权减去in[v],然后将这个环缩成一个点,然后迭代进行，直至到达根节点r，这样还是O(nm)。
    • 考虑优化，我们对于每个点x建一棵左偏树$T_x$，然后我们就可以在O(1)的时间复杂度查询一个节点的最小入边，缩环的时候直接合并左偏树即可，边权减打标记即可,因此我们需要很好的实现标记下放，一次对环的合并我们不妨及做log(n)，每个节点属于哪个环可以用并查集路径压缩+按秩合并，删除节点可以用延迟删除($N_5$)，那么最终时间复杂度不难分析的出来是O(m+nlog(n))。
    • 求没有确定的根的树形图:建立一个超级根r，以它为根跑算法,只要将r向原图每个点连接一条权值大于原图中所有边的边权的边，这样选这些边肯定不划算，因此只会选择一条。
    • 判无解的奇技淫巧:从小到大依次枚举每个点i,加入边$(i,(i+1)\%n+1,+∞)$,这样如果你最后得到的答案为+∞，那么就无解了。

2. 应用

  • 不确定根的最小树形图：

    这次我们不规定树形图的根，要求最小树形图。

    容易发现我们建立一个超级源点，然后向每一个结点连长度为 infinf 的边，最后算出答案后减去 infinf 即可。发现为了使答案更优，最多只会从超级源点连出一条边，从而保证了去掉超级源点后的根是唯一的。

    时间复杂度 O(nm)。

  • 滑雪

    朴素算法不能通过，考虑利用这题的性质。我们先搜出能够到达的所有点，再将边以终点高度为第一关键字，边权为第二关键字排序后，跑 Kruskal 即可。时间复杂度 O(mlogm)。