20220108-最近公共祖先
最近公共祖先
1. 基本概念
- 定义:树上任意两点向根节点靠近的路上重合的深度最大的点;
图示定义 :蓝色节点和粉色节点的最近公共祖先是绿色点;
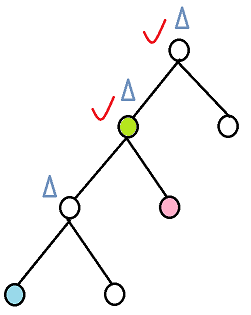
2. 求解LCA方法
向上标记法:暴力。两个节点平层同时向上跳,直到相遇,相遇的点即为LCA。如果有m次查询,那么时间复杂度为
O(mn)。倍增法:如果使用暴力算法求解,对于深度较大的树需要很久的时间,考虑采用倍增的方式来优化,具体而言:
- 符号表示:
fa[i, j]:表示从i开始,向上走$2^j$步,即表示节点i的第j+1位祖先。其中$0\le j\le \log n$;depth[i]:表示深度;- 哨兵:从
i开始,向上走$2^j$步,如果跳过根节点,则fa[i, j] = 0,depth[0] = 0(表示节点0是第0层)。
- 步骤:
- 先将两个点跳到同一层;
- 让两个点同时往上跳,一直跳到它们的最近公共祖先的下一层;
- 时间复杂度:预处理$O(n\log n)$、查询$O(\log n)$。
- 注:这里倍增的思想一部分来自整数拼凑(11 = 8 + 2 + 1 = 1011)。我们知道如果
fa[i,k]==fa[j,k],则说明在跳了$2^k$步之后找到了公共祖先,但是该节点不一定是最近的;但反之,如果fa[i,k]!=fa[j,k],则说明节点i和节点j还没有找到公共祖先。
- 符号表示:
Tarjan:优雅的离线求LCA做法,时间复杂度为
O(m + n)。在线算法:读入一个输入,得到一个输出;
离线算法:将输入全部读入,之后才处理输出;
本质:对向上标记算法的优化。
思想:首先深度优先遍历:
如果当前节点涉及到某一个询问,且询问的另一个点已经访问过,则可以得出答案;
反之,标记节点
x已访问过,直到访问到另一个节点。举例:假设询问为节点4和节点9,从根节点出发,访问到x并标记已访问;发现节点9并没有被访问,所以不管,继续走;回溯,遍历,当遇到9的时候,发现另一个点4已经访问过了,所以此时两个点的LCA就是更新到了的4的祖先,节点1。
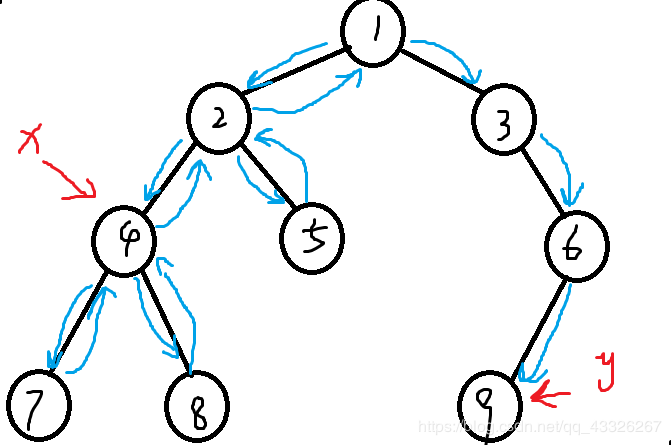
如果在回溯的时候更新祖先节点,假设fa[x]为点x的祖先节点,从节点1→节点2→节点4→节点7,到达叶子节点之后回溯,标记
fa[7] = 4;再遍历到节点8回溯,标记fa[8] = 4;继续回溯,标记fa[4] = 2;再遍历到节点5回溯,标记fa[5] = 2……随着回溯的当前层数越浅,各个节点最终指向的祖先也越来越高,所以如果另一个节点已经标记,说明那个点的祖先就一定时两个点的LCA。同时,在访问到一个点时,可以一并解决所有与这个点有关的询问,所以可以使用邻接表或向量来进行存储。该思路基于深度优先遍历,可以将所有的点分为3类 :
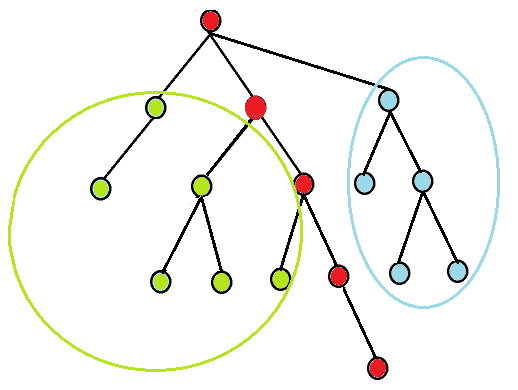
- 第1类:未被搜索过的点;
- 第2类:正在搜索的分支;
- 第3类:已经遍历过,且回溯过的点;
其中第2类和第3类节点已经通过并查集合并成一个集合,因此具体步骤如下:
- 在进入递归层时,将点标记为
1; - 搜索所有没有遍历过的边且与该点连接的点,搜索回溯后,完成集合合并;
- 将所有与该层点有关系的询问,全部遍历,当另一个点已经被标记为2,则找到了最近公共祖先,就是另一个点的并查集标记节点;
- 最后回溯时,将该节点标记为2;
注意:先将要拓展的节点展开,回溯时再进行集合合并。
首先求出所有点到根节点的距离
depth[],设节点x和节点y的最近公共祖先是p, 则节点x和节点y的最近距离为depth[x] + depth[y] - 2* depth[p];- 在深度优先遍历
1号节点中的节点u时,需要把节点u的查询的另外一个点的最短距离进行计算并存储,最后把节点u合并到上一节点的集合。
树剖:把一棵树按子树大小分为链。【参考】
基本操作:求x到y的路径边权和(或对所有边权进行修改);
启发:可以使用树剖思路解决LCA。具体而言,直接判断节点x和节点y是否在同一条链上:
- 若不在同一条链上,则深度较大的节点跳转到链头的父节点,即跳出这条链;
- 若在同一条链上,则深度较浅的节点即为LCA。
定理:对于一张无向图,如果存在最小生成树和(严格)次小生成树,那么对于任何一颗最小生成树,都存在一棵(严格)次小生成树,使得这两棵树只有一条边不同。
3. 经典例题
祖孙询问(倍增法)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
using namespace std;
const int N = 40010, M = 2 * N;
int n, m;
int h[N], e[M], ne[M], idx;
int depth[N], fa[N][26];
void add(int a, int b){
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
void bfs(int root){
memset(depth, 0x3f, sizeof depth);
depth[0] = 0, depth[root] = 1;
queue<int> q;
q.push(root);
while(q.size()){
int t = q.front(); q.pop();
for(int i = h[t]; i != -1; i = ne[i]){
int j = e[i];
if(depth[j] > depth[t] + 1){ // 说明j还没有被搜索过
depth[j] = depth[t] + 1;
q.push(j);
fa[j][0] = t; // 节点j的父节点为t
for(int k = 1; k <= 15; k++){
//从j跳2^k步长的距离,相当于从j连续跳两个2^(k-1)步长的距离
fa[j][k] = fa[fa[j][k - 1]][k - 1];
}
}
}
}
}
int lca(int a, int b){
// 保证a在b的下面
if(depth[a] < depth[b]) swap(a, b);
// 移动a,使得a和b平层
for(int k = 15; k >= 0; k--){
if(depth[fa[a][k]] >= depth[b]){
a = fa[a][k];
}
}
if(a == b) return a;
// 利用整数拼凑的思想,节点a和节点b同时上移直到找到公共节点
for(int k = 15; k >= 0; k--){
if(fa[a][k] != fa[b][k]){
a = fa[a][k];
b = fa[b][k];
}
}
// 循环结束,到达LCA下一层
return fa[a][0]; // 返回节点a的父节点
}
int main(){
cin>>n;
int root = 0;
memset(h, -1, sizeof h);
for(int i = 0; i < n; i++){
int a, b; cin>>a>>b;
if(b == -1) root = a;
else add(a, b), add(b, a);
}
bfs(root); // 建树
cin>>m;
while(m--){
int a, b; cin>>a>>b;
int p = lca(a, b);
if(p == a) puts("1");
else if(p == b) puts("2");
else puts("0");
}
return 0;
}
距离(Tarjan算法)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
using namespace std;
typedef pair<int, int> PII;
const int N = 10010, M = N * 2;
int n, m;
int h[N], e[M], ne[M], w[M], idx;
int dist[N], p[N], res[M], st[N];
vector<PII> query[N]; // [查询另一个点, 查询序号]
void add(int a, int b, int c){
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}
void dfs(int u, int fa){
for(int i = h[u]; i != -1; i = ne[i]){
int j = e[i];
if(j == fa) continue;
dist[j] = dist[u] + w[i];
dfs(j, u);
}
}
int find(int x){
if(p[x] != x) p[x] = find(p[x]);
return p[x];
}
void tarjan(int u){
st[u] = 1; // 标记当前正在搜索的点
for(int i = h[u]; i != -1; i = ne[i]){ // 遍历所有邻点
int j = e[i];
if(!st[j]){
tarjan(j);
p[j] = u; // 将节点j合并到父节点u中
}
}
for(auto item: query[u]){
int y = item.first, id = item.second;
if(st[y] == 2){
int anc = find(y);
res[id] = dist[u] + dist[y] - dist[anc] * 2;
}
}
st[u] = 2;
}
int main(){
cin>>n>>m;
memset(h, -1, sizeof h);
for(int i = 0; i < n - 1; i++){
int a, b, c; cin>>a>>b>>c;
add(a, b, c), add(b, a, c);
}
for(int i = 0; i < m; i++){
int a, b; cin>>a>>b;
if(a != b){ // 二者不相等的时候才需要记录查询
query[a].push_back({b, i});
query[b].push_back({a, i});
}
}
for(int i = 1; i <= n; i++) p[i] = i;
dfs(1, -1); // 初始化dist数据,处理每个点和1号节点的距离
tarjan(1); // 随便拿一个点当作根节点
for(int i = 0; i < m; i++) cout<<res[i]<<endl;
return 0;
}