20220108-树链剖分

发表于 更新于 阅读次数： 本文字数： 579 阅读时长 ≈ 1 分钟

树链剖分

1. 基本概念

  • 树链剖分（简称树剖）；

  • 重儿子：这里我理解为重（zhòng）儿子，因为它是某个节点众多子树中权值最大的子树的根节点。从该节点连向重儿子的边即为重边。

    img

  • 重链：由重边连接的点和边组成，即为树链；

2. 树链的性质

  • 一条树链必是一个轻儿子或根节点开头，通过重边串起来一部分重儿子；
  • 一个非叶子节点只有一个重儿子；
  • 单独的叶子节点是一条树链，满足以轻儿子开头。因此一棵树必定可被划分为几条树链；

3. 边转点

  • 树剖+线段树：可以维护树上的点权区间；

  • 边转点：将边权转化为点权。可以维护边权区间；

  • 操作：由于每个点的父节点唯一，因此将边权给深度更大的那个点。

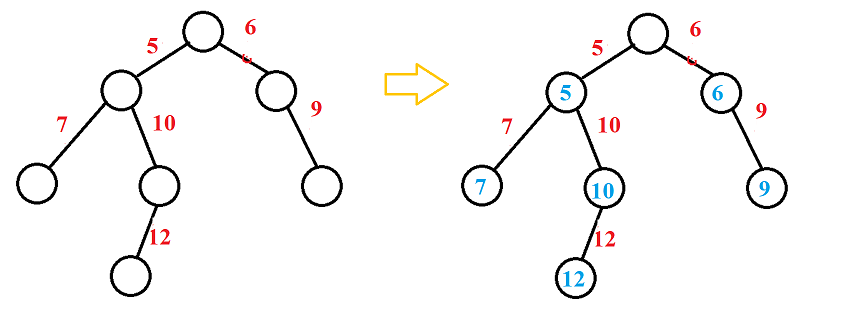
    image-20220108213833462.png

    从上面的图来看，第一个点没有值。因此需要注意：

    • 当完成边化点线段树维护操作后进行查询操作时，搜索范围应从2开始（或者赋值第一个点为极大值）；
    • 由于每个点对应的边都是它到它父亲节点的边，所以在查询区间或修改区间时不能考虑LCA，区间应为[dfn[son[lca]], dfn[]]。

4. 经典例题：树链剖分

  • 题意：共有4种操作：

    • 1 x y z：表示将树从x到y节点最短路径上所有节点的值都加上z；
    • 2 x y：表示求树从x到y节点最短路径上所有节点的值之和；
    • 3 x z：表示将以x为根节点的子树内所有节点值都加上z；
    • 4 x：表示求以x为根节点的子树内所有节点值之和。

  • 思路：采用LCA，可以先让两个点同时往上跳，直到某个值相同，之后可以一起操作。