20220109-线段树

发表于 阅读次数： 本文字数： 410 阅读时长 ≈ 1 分钟

线段树

1. 基本概念

  • 定义：线段树是一棵满二叉树（除了最后一层），因此可以用堆（一维数组）进行存储；

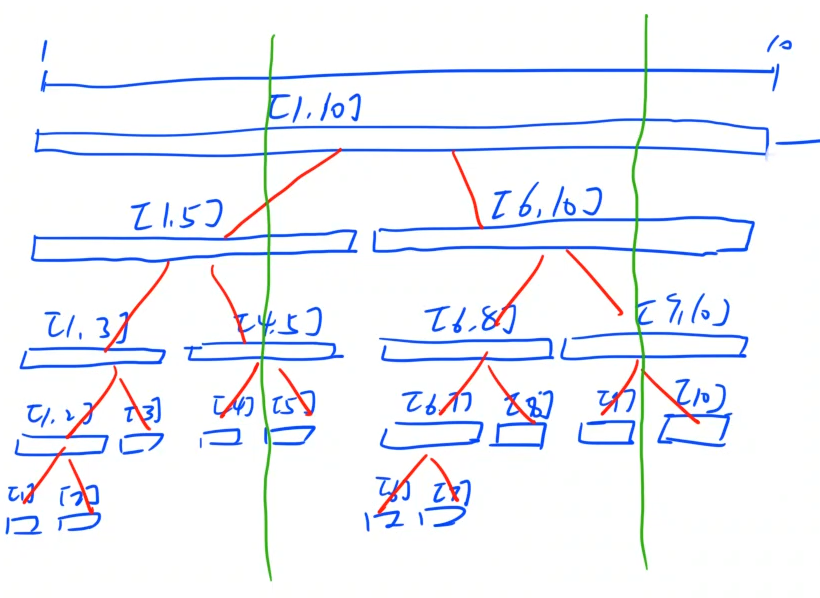
    image-20210812114439710.png

    对于上图中的段，从上到下，从左到右依次编号1，2，3，……

    对于某一段u：

    • 父节点为$\left\lfloor x/2 \right\rfloor $，即u>>1；
    • 左儿子为（$2x$），即u<<1；
    • 右儿子为（$2x+1$），即u<<1 | 1；

    同时在考虑存储空间时，倒数第二层最多有n个节点，倒数第一层最多有2n个节点，倒数第二层之前最多有(n-1)个节点，因此最多总共有(4n-1)个节点。因此我们需要开$4n$大小的空间。

  • 5种基本操作：
    • push_up：由子节点计算父节点，sum = L.sum + R.sum；
    • push_down：将父节点修改信息下传至子节点，也被称作懒标记（或延迟标记）；
    • build：将一段区间初始化为线段树；
    • modify：修改端点或修改区间。
    • query：查询某一段区间的信息。
  • 扫描线法