20220109-Polya.How to solve it
[方法论] - How to solve it
- 弄清问题
- 未知数是什么？已知数是什么？条件是什么？【输入 + 输出 + 约束】
- 满足条件是否可能？要确定未知数，条件是否充分？或者多余？还是矛盾？
- 画一张图，使用恰当的符号；
- 理清不同的条件，并尝试记录它们；
- 拟定计划
- 找出已知数和未知数之间的联系。如果没有直接的联系，就必须先考虑辅助性的问题。最终得到一个求解计划。
- 你以前见过它吗？是否见过相同的或者形式稍有不同的问题？
- 是否知道与此相关的问题？或者一个可以用得上的定理？
- 看着未知数，想出一个有相同或者相似未知数的熟悉问题。
- 如果有一个与现在的问题有关并且早已解决的问题，你能否利用它？能否利用它的结果或方法？为了利用它是否应该先引入某些辅助元素？
- 能否重新叙述这个问题，尽可能地从不同的角度？很多时候必须回到定义中去。
- 如果你不能解决所提出的问题，可以尝试先解决一个与此有关的。你能否提出一个更容易着手的相关问题——像是一个更普遍的或者更特殊的，或者一个类比的问题？
- 能否解决这个问题的一部分？仅仅保留条件的一部分而舍弃其余，这样对于未知数能确定到什么程度？它还能怎样变化？你能否从已知数据推导出来某些有用的信息？你是否考虑过用其他数据来确定未知数？如果需要的话，你能否转化未知数或数据（或者二者同时），以使得新未知数和新数据联系更紧密？
- 你是否利用了所有的已知数据？你是否利用了全部的条件？你是否考虑了问题种包含的所有基本概念？
- 找出已知数和未知数之间的联系。如果没有直接的联系，就必须先考虑辅助性的问题。最终得到一个求解计划。
- 实行计划
- 实现你的解题计划，检查每个步骤。你能否清楚地看出这一步骤的正确性？你能否证明？
- 回顾
- 验算所得到的解
- 你能否验算这个解？能否解决争议？
- 你能否用别的方法得到这个解答？或者你其实能否一眼就看出它来？
- 你能否把本题的结果或方法应用于其他的问题？
- 验算所得到的解
20220109-线段树
线段树
1. 基本概念
定义：线段树是一棵满二叉树（除了最后一层），因此可以用堆（一维数组）进行存储；
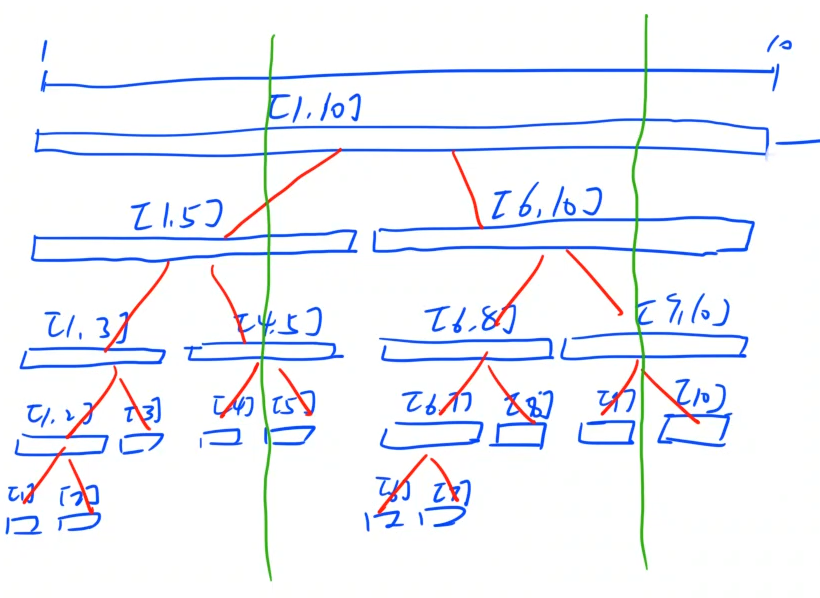
对于上图中的段，从上到下，从左到右依次编号1，2，3，……
对于某一段
u：- 父节点为$\left\lfloor x/2 \right\rfloor $，即
u>>1； - 左儿子为（$2x$），即
u<<1； - 右儿子为（$2x+1$），即
u<<1 | 1；
同时在考虑存储空间时，倒数第二层最多有n个节点，倒数第一层最多有2n个节点，倒数第二层之前最多有(n-1)个节点，因此最多总共有(4n-1)个节点。因此我们需要开$4n$大小的空间。
- 父节点为$\left\lfloor x/2 \right\rfloor $，即
- 5种基本操作：
push_up：由子节点计算父节点，sum = L.sum + R.sum；push_down：将父节点修改信息下传至子节点，也被称作懒标记（或延迟标记）；build：将一段区间初始化为线段树；modify：修改端点或修改区间。query：查询某一段区间的信息。
- 扫描线法
